Analysis of Analog Circuits

Negative feedback amplifier

When a fraction of the output of an amplifier is combined with the input, feedback exists; if the feedback opposes the original signal, it is negative feedback and if it increases the signal it is positive feedback. A negative feedback amplifier, or more commonly simply a feedback amplifier, is an amplifier which uses negative feedback to improve performance (gain stability, linearity, frequency response, step response) and reduce sensitivity to parameter variations due to manufacturing or environmental uncertainties. A single feedback loop with unilateral blocks is shown in Figure 1. Negative feedback is used in this way in many amplifiers and control systems.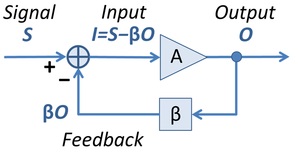

Figure 1: Ideal negative feedback model

Classical feedback

Voltage amplifiers

Below, the gain of the amplifier with feedback, the closed-loop gain A_fb, is derived in terms of the gain of the amplifier without feedback, the open-loop gain A_OL and the feedback factor β, which governs how much of the output signal is applied to the input. See Figure 1, top right. The feedback parameter β is determined by the feedback network that is connected around the amplifier. For an operational amplifier two resistors may be used for the feedback network to set β between 0 and 1. This network may be modified using reactive elements like capacitors or inductors to (a) give frequency-dependent closed-loop gain as in equalization/tone-control circuits or (b) construct oscillators.
Consider a voltage amplifier with voltage feedback. Without feedback, the output voltage V_out = A_OL V_in, where the open-loop gain A_OL in general may be a function of both frequency and voltage. The open-loop gain A_OL is defined by:

where V_in is the input to the amplifier, assuming no feedback, and V_out is the amplifier output, again with no feedback.
Suppose we have a feedback loop so that a fraction β V_out of the output is subtracted from the input. The input to the amplifier is now V'_in, where

The gain of the amplifier with feedback, called the closed-loop gain, A_fb is given by,

Substituting for V_in,

Dividing numerator and denominator by V'_in,

But since

,

then

If A_OL >> 1, then A_fb ≈ 1 / β and the effective amplification (or closed-loop gain) A_fb is set by the feedback constant β, and hence set by the feedback network, usually a simple reproducible network, thus making linearizing and stabilizing the amplification characteristics straightforward. Note also that if there are conditions where β A_OL = −1, the amplifier has infinite amplification – it has become an oscillator, and the system is unstable. The stability characteristics of the gain feedback product β A_OL are often displayed and investigated on a Nyquist plot (a polar plot of the gain/phase shift as a parametric function of frequency). A simpler, but less general technique, uses Bode plots.
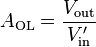The combination L = β A_OL appears commonly in feedback analysis and is called the loop gain. The combination ( 1 + β A_OL ) also appears commonly and is variously named as the desensitivity factor or the improvement factor.
Bandwidth extension

Figure 2: Gain vs. frequency for a single-pole amplifier with and without feedback; corner frequencies are labeled.

Feedback can be used to extend the bandwidth of an amplifier (speed it up) at the cost of lowering the amplifier gain. Figure 2 shows such a comparison. The figure is understood as follows. Without feedback the so-called open-loop gain in this example has a single time constant frequency response given by

where f_C is the cutoff or corner frequency of the amplifier: in this example f_C = 10⁴ Hz and the gain at zero frequency A₀ = 10⁵ V/V. The figure shows the gain is flat out to the corner frequency and then drops. When feedback is present the so-called closed-loop gain, as shown in the formula of the previous section, becomes,

The last expression shows the feedback amplifier still has a single time constant behavior, but the corner frequency is now increased by the improvement factor ( 1 + β A₀ ), and the gain at zero frequency has dropped by exactly the same factor. This behavior is called the gain-bandwidth tradeoff. In Figure 2, ( 1 + β A₀ ) = 10³, so A_fb(0)= 10⁵ / 10³ = 100 V/V, and f_C increases to 10⁴ × 10³ = 10⁷ Hz.

Multiple poles

When the open-loop gain has several poles, rather than the single pole of the above example, feedback can result in complex poles (real and imaginary parts). In a two-pole case, the result is peaking in the frequency response of the feedback amplifier near its corner frequency, and ringing and overshoot in its step response. In the case of more than two poles, the feedback amplifier can become unstable, and oscillate. See the discussion of gain margin and phase margin. For a complete discussion, see Sansen.
Feedback and amplifier type
Amplifiers use current or voltage as input and output, so four types of amplifier are possible. See classification of amplifiers. Any of these four choices may be the open-loop amplifier used to construct the feedback amplifier. The objective for the feedback amplifier also may be any one of the four types of amplifier, not necessarily the same type as the open-loop amplifier. For example, an op amp (voltage amplifier) can be arranged to make a current amplifier instead. The conversion from one type to another is implemented using different feedback connections, usually referred to as series or shunt (parallel) connections. See the table below.

The feedback can be implemented using a two-port network. There are four types of two-port network, and the selection depends upon the type of feedback. For example, for a current feedback amplifier, current at the output is sampled and combined with current at the input. Therefore, the feedback ideally is performed using an (output) current-controlled current source (CCCS), and its imperfect realization using a two-port network also must incorporate a CCCS, that is, the appropriate choice for feedback network is a g-parameter two-port.

Two-port analysis of feedback

One approach to feedback is the use of return ratio. Here an alternative method used in most textbooks is presented by means of an example treated in the article on asymptotic gain model.

Figure 3: A shunt-series feedback amplifier

Figure 3 shows a two-transistor amplifier with a feedback resistor R_f. The aim is to analyze this circuit to find three items: the gain, the output impedance looking into the amplifier from the load, and the input impedance looking into the amplifier from the source.

Replacement of the feedback network with a two-port

The first step is replacement of the feedback network by a two-port. Just what components go into the two-port?
On the input side of the two-port we have R_f. If the voltage at the right side of R_f changes, it changes the current in R_f that is subtracted from the current entering the base of the input transistor. That is, the input side of the two-port is a dependent current source controlled by the voltage at the top of resistor R₂.
One might say the second stage of the amplifier is just a voltage follower, transmitting the voltage at the collector of the input transistor to the top of R₂. That is, the monitored output signal is really the voltage at the collector of the input transistor. That view is legitimate, but then the voltage follower stage becomes part of the feedback network. That makes analysis of feedback more complicated.

Figure 4: The g-parameter feedback network

An alternative view is that the voltage at the top of R₂ is set by the emitter current of the output transistor. That view leads to an entirely passive feedback network made up of R₂ and R_f. The variable controlling the feedback is the emitter current, so the feedback is a current-controlled current source (CCCS). We search through the four available two-port networks and find the only one with a CCCS is the g-parameter two-port, shown in Figure 4. The next task is to select the g-parameters so that the two-port of Figure 4 is electrically equivalent to the L-section made up of R₂ and R_f. That selection is an algebraic procedure made most simply by looking at two individual cases: the case with V₁ = 0, which makes the VCVS on the right side of the two-port a short-circuit; and the case with I₂ = 0. which makes the CCCS on the left side an open circuit. The algebra in these two cases is simple, much easier than solving for all variables at once. The choice of g-parameters that make the two-port and the L-section behave the same way are shown in the table below.

http://en.wikipedia.org/wiki/Negative_feedback_amplifier
Rooselvet Ramirez  EES

Cuadripolo o Redes de dos Puertos

Cuadripolo Se llama cuadripolo a una red (circuito eléctrico) con dos puertos (o dos pares de polos), considerada como una "caja negra" y caracterizada por una serie de parámetros, relacionados con las impedancias que presenta en cada una de las puertas y con su función de transferencia. La palabra bipuerto es, en realidad, más general que cuadripolo, piense por ejemplo en una guía de onda formada por un único conductor hueco, en este caso cada extremo de la guía es un puerto de acceso a la línea, donde se puede realizar un intercambio energético, pero es evidente que no puede identificarse 2 polos por cada puerto de acceso. El cuadripolo es un modelo muy potente para caracterizar componentes o secciones de circuitos (amplificadores, filtros, etc), de modo que no hace falta descender hasta el nivel de componente a la hora de analizar una red grande. Los parámetros más utilizados cuando se habla de cuadripolos son, entre otros: Impedancias y admitancias de las puertas. Impedancia característica. Pérdidas de inserción. Función de transferencia. Aunque el cuadripolo representa un circuito de topología arbitraria, muchas veces conviene relacionar sus parámetros con una topología determinada. Por ello existe la serie de topologías características de los cuadripolos siguiente: Red en "T": Consta de dos impedancias, Z1 y Z2, que conectan la puerta 1 con la puerta 2. Entre Z1 y Z2 se dispone la impedancia ZP conectada al nodo común a ambas puertas (a). Red en "T" puenteada. Es una red en "T" con una impedancia ZS conectando directamente ambas puertas Red en "pi". Es la red dual de la "T": Z1 y Z2 conectan cada puerta al nodo común. mientras ZS interconecta ambas puertas (b). Red en celosía. Esta red no tiene un nodo común a ambas puertas. Consiste en dos impedancias, ZS1 y ZS2, conectando los nodos de una puerta a la otra, y otras dos, ZP1 y ZP2, conectando ambas puertas, de modo que enlacen los nodos de ZS1 con y ZS2 (c). Topología de cuadripolos. Matrices La existencia de ocho a nueve puertas hace que parámetros como la impedancia de una puerta dependa de lo que haya conectado en la otra. Considerando un cuadripolo que sea un cable sin resistencia que conecte ambas puertas, en una de ellas se verá la impedancia que haya conectada en la otra. Por ello se emplean parámetros matriciales que son los siguientes: Impedancias, matriz Z Los términos de Z vienen dados por las expresiones siguientes: Admitancias, matriz Y Los términos de Y vienen dados por las expresiones siguientes: Parámetros híbridos, H Los términos de H vienen dados por las expresiones siguientes: Los parámetros H son muy apropiados para la descripción del transistor. En particular β es h21, y así suele aparecer en las hojas de datos (HFE) Parámetros híbridos, G Los términos de G vienen dados por las expresiones siguientes: Los parámetros G son muy apropiados para la descripción de las válvulas termoiónicas. Parámetros T Los parámetros T expresan las magnitudes de una puerta en función de las de la otra. Son útiles para la conexión de cuadripolos en cascada. Análisis Para el cálculo de los parámetros de un cuadripolo es necesario resolver el circuito que lo compone y, conocidos v1, v2, i1 e i2, se puede obtener cualquiera de las matrices. Pero para hacer esto, se puede optar por una estrategia que simplifica los cálculos. Supongamos que queremos calcular (Z). De las expresiones anteriores, vemos que si Y, haciendo lo que permite obtener (Z) sin necesidad de calcular toda la red. Del mismo modo, haciendo v1 = 0 y v2 = 0, se calcula (Y). Para los híbridos se elige, igualmente, el parámetro que se debe anular. Las corrientes se anulan dejando la puerta del cuadripolo sin conexión, mientras que las tensiones se anulan cortocircuitando el terminal. En la práctica, esto se realiza mediante ensayos. Interconexión de cuadripolos Del mismo modo que los demás componentes de un circuito, los cuadripolos se pueden conectar entre ellos para obtener otros cuadripolos más complejos. Se estudian las siguientes formas: Paralelo-paralelo. En la figura, (a). La tensión v1 es común a ambos cuadripolos y la v2, también. (YT) = (Y1) + (Y2). Serie-serie. En la figura, (b). La corriente i1 es igual en las puertas de los dos cuadripolos y la i2, también. (ZT) = (Z1) + (Z2). Paralelo-serie. En la figura, (c). La tensión v1 es común a ambos cuadripolos y la corriente i2, también. (GT) = (G1) + (G2). Serie-paralelo. En la figura, (d). La corriente i1 es igual en las puertas de los dos cuadripolos y la tensión v2, también. (HT) = (H1) + (H2). Cascada. La salida del segundo cuadripolo se conecta a la entrada del primero. Como el producto de matrices no es conmutativo, es importante seguir este criterio. (FT) = (F1) · (F2). Cabe aclarar que la aplicación del Test de Brune NO es razón suficiente para determinar que dos cuadripolos NO se pueden interconectar en alguna de las configuraciones anteriormente nombradas, excluyendo la conexión en cascada la cual no requiere de la verificación por el Test de Brune, en efecto, no cumplir el Test de Brune en las configuraciones que así lo requieran implica que los parámetros del cuadripolo resultante no se pueden determinar por medio de las matrices de cada cuadripolo con las sumas de estas (los parámetros a sumar dependen del tipo de conexión).   Representación conceptual de la interconexión de cuadripolos. Acoplamiento entre cuadripolos Eliminación de la corriente entre los cuadripolos. En realidad, en el caso de cuadripolos en serie, puede existir la corriente marcada en rojo en la figura 3-(a), que se cierra entre ellos, pero no pasa por los teminales del cuadripolo serie. Para evitarlo se introduce el transformador de (b). Limitaciones del modelo Debido a que el modelo se basa en consideraciones lineales de los circuitos (los coeficientes de las matrices características son constantes), en la mayoría de los casos sólo es aplicable este concepto a rangos limitados de frecuencias y a condiciones estables, donde justamente estos parámetros no varían en el circuito real. Sin embargo, puede modelarse un circuito como un cuadripolo distinto para distintos intervalos de frecuencias con distintos parámetros, al igual que con distintas condiciones externas: excitación, temperatura, etc. No siempre es posible encontrar los modelos (o matrices asociadas) de cuadripolo para cualquier circuito. En ocasiones sólo es posible, por ejemplo, hallar la matriz de impedancias y no la de admitancias. Nótese que Z = Y − 1. Por lo que si Y es no inversible, no existe Z. http://es.wikipedia.org/wiki/Cuadripolo Rooselvet Ramirez EES

Device Model

Models for device design

The modern transistor has an internal structure that exploits complex physical mechanisms. Device design requires a detailed understanding of how device manufacturing processes such as ion implantation, impurity diffusion, oxide growth, annealing, and etching affect device behavior. Process models simulate the manufacturing steps and provide a microscopic description of device "geometry" to the device simulator. By "geometry" is meant not only readily identified geometrical features such as whether the gate is planar or wrap-around, or whether the source and drain are raised or recessed (see Figure 1 for a memory device with some unusual modeling challenges related to charging the floating gate by an avalanche process), but also details inside the structure, such as the doping profiles after completion of device processing.

Figure 1: Floating-gate avalanche injection memory device FAMOS

With this information about what the device looks like, the device simulator models the physical processes taking place in the device to determine its electrical behavior in a variety of circumstances: DC current-voltage behavior, transient behavior (both large-signal and small-signal), dependence on device layout (long and narrow versus short and wide, or interdigitated versus rectangular, or isolated versus proximate to other devices). These simulations tell the device designer whether the device process will produce devices with the electrical behavior needed by the circuit designer, and is used to inform the process designer about any necessary process improvements. Once the process gets close to manufacture, the predicted device characteristics are compared with measurement on test devices to check that the process and device models are working adequately.

Although long ago the device behavior modeled in this way was very simple - mainly drift plus diffusion in simple geometries - today many more processes must be modeled at a microscopic level; for example, leakage currents in junctions and oxides, complex transport of carriers including velocity saturation and ballistic transport, quantum mechanical effects, use of multiple materials (for example, Si-SiGe devices, and stacks of different dielectrics) and even the statistical effects due to the probabilistic nature of ion placement and carrier transport inside the device. Several times a year the technology changes and simulations have to be repeated. The models may require change to reflect new physical effects, or to provide greater accuracy. The maintenance and improvement of these models is a business in itself.
These models are very computer intensive, involving detailed spatial and temporal solutions of coupled partial differential equations on three-dimensional grids inside the device. Such models are slow to run and provide detail not needed for circuit design. Therefore, faster transistor models oriented toward circuit parameters are used for circuit design.
Functional model of an NPN transistor
The operation of a transistor is difficult to explain and understand in terms of its internal structure. It is more helpful to use this functional model:

• The base-emitter junction behaves like a diode.
  
• A base current I_B flows only when the voltage V_BE across the base-emitter junction is 0.7V or more.
  
• The small base current I_B controls the large collector current Ic.
  
• Ic = h_FE × I_B   (unless the transistor is full on and saturated)
  h_FE is the current gain (strictly the DC current gain), a typical value for h_FE is 100 (it has no units because it is a ratio)
  
• The collector-emitter resistance R_CE is controlled by the base current I_B:
• I_B = 0   R_CE = infinity   transistor off
  
• I_B small   R_CE reduced   transistor partly on
  
• I_B increased   R_CE = 0   transistor full on ('saturated')

Additional notes:

• A resistor is often needed in series with the base connection to limit the base current I_B and prevent the transistor being damaged.
  
• Transistors have a maximum collector current Ic rating.
  
• The current gain h_FE can vary widely, even for transistors of the same type!
  
• A transistor that is full on (with R_CE = 0) is said to be 'saturated'.
  
• When a transistor is saturated the collector-emitter voltage V_CE is reduced to almost 0V.
  
• When a transistor is saturated the collector current Ic is determined by the supply voltage and the external resistance in the collector circuit, not by the transistor's current gain. As a result the ratio Ic/I_B for a saturated transistor is less than the current gain h_FE.
  
• The emitter current I_E = Ic + I_B, but Ic is much larger than I_B, so roughly I_E = Ic.

http://en.wikipedia.org/wiki/Transistor_models

http://www.kpsec.freeuk.com/trancirc.htm

Rooselvet Ramirez EES

Basic Single-Transistor Amplifier

Transistor as an amplifier

The common-emitter amplifier is designed so that a small change in voltage in (V_in) changes the small current through the base of the transistor and the transistor's current amplification combined with the properties of the circuit mean that small swings in V_in produce large changes in V_out.

Various configurations of single transistor amplifier are possible, with some providing current gain, some voltage gain, and some both.

From mobile phones to televisions, vast numbers of products include amplifiers for sound reproduction, radio transmission, and signal processing. The first discrete transistor audio amplifiers barely supplied a few hundred milliwatts, but power and audio fidelity gradually increased as better transistors became available and amplifier architecture evolved.

Modern transistor audio amplifiers of up to a few hundred watts are common and relatively inexpensive.

Advantages

The key advantages that have allowed transistors to replace their vacuum tube predecessors in most applications are

• Small size and minimal weight, allowing the development of miniaturized electronic devices.
• Highly automated manufacturing processes, resulting in low per-unit cost.
• Lower possible operating voltages, making transistors suitable for small, battery-powered applications.
• No warm-up period for cathode heaters required after power application.
• Lower power dissipation and generally greater energy efficiency.
• Higher reliability and greater physical ruggedness.
• Extremely long life. Some transistorized devices have been in service for more than 30 years.
• Complementary devices available, facilitating the design of complementary-symmetry circuits, something not possible with vacuum tubes.
• Insensitivity to mechanical shock and vibration, thus avoiding the problem of microphonics in audio applications.

Limitations

• 
  
  Silicon transistors do not operate at voltages higher than about 1,000 volts (SiC devices can be operated as high as 3,000 volts). In contrast, electron tubes have been developed that can be operated at tens of thousands of volts.
• 
  
  High power, high frequency operation, such as that used in over-the-air television broadcasting, is better achieved in electron tubes due to improved electron mobility in a vacuum.
• 
  
  Silicon transistors are much more sensitive than electron tubes to an electromagnetic pulse, such as generated by an atmospheric nuclear explosion.

http://www.ngsir.netfirms.com/englishhtm/Amplifier.htm

http://en.wikipedia.org/wiki/Transistor

Rooselvet Ramirez   EES

Super Source Follower

Super Source Follower

Reduce output resistence of source follower, useful if you need to drive a resitive load.

Small signal 

output resistence:

http://kaflatooni.yasna.com/single_transistor_amp.pdf

http://organics.eecs.berkeley.edu/~viveks/ee140/lectures/section10p4.pdf

Rooselvet Ramirez EES

Differential Amplifier

Differential Amplifier

Before getting into differential amplifiers, let's review small-signal transistor models, and introduce a new one that will be of service. In the figure below, the new model is on the right, and our familiar models on the left. The resistances r_π an

d r_e both are related to how much the output current changes with respect to input voltage, and the relations of them to the general parameter, the transconductance g_m, are shown. Once you know the bias collector current, you can calculate these important parameters.

In the new model, which we may call the alpha model, the direct connection of the base may worry you. However, note that the current-controlled current source in the collector makes sure that only the proper base current flows. In the (good) approximation that α = 1, there will be no base current at all. The connection to this internal, inaccessible node is only to put the base-emitter voltage across the resistor r_e to make the emitter current. The collector then takes what it likes, leaving the rest for the base. In fact, alpha is often taken as unity when you use the alpha model for quick insight, for which it is specially adapted.

There are two inputs and two outputs, and the circuit is assumed to be symmetrical, which it always is in practice, to a first approximation. If only one output is used, the other collector resistor can be eliminated, with no change to the functioning of the circuit. It is very convenient to express the inputs as the sum of a common-mode input v_cm, which is the average of the two input voltages, and the differential mode input v_d. In the common mode, the same voltage v_cm is applied to the two inputs. In the differential mode, opposite and equal voltages &plusmi;v_d are applied to the two inputs.
In the common mode, the amplifier acts as a single amplifier with collector resistance R_C/2 and emitter resistance R_S + (R_E + r_e)/2, so the gain (the ratio of the resistances), input impedance and output impedance can easily be found, as for the single-transistor amplifier. If the input is taken single-ended, the gain is R_E/(2R_S + R_E + r_e). R_S is usually made very large, so that the common-mode gain is small. In many cases, R_S is actually replaced by a current source that has a very high internal resistance, so the common-mode gain is practically zero. This means that the amplifier will not respond to any signal common to the two inputs, which is generally desirable.
In the differential mode, the symmetry of the inputs means that node "a" will not change in voltage, and i₁ = -i₂ = v_d/(2R_E + 2r_e). From this result, the gain at an output node is easily found: G = R_C/2R_E + 2r_e). This is called the single-ended gain. If the output is taken between the two collectors (double-ended) the gain is twice this value. Note that we have inverting and noninverting outputs as well as inputs. The differential input simply divides the same total current between the two sides of the amplifier. It can go no farther than to put all the current through one collector or the other, however.
Consider a circuit in which the input is to v₁, the other input grounded, and the output is taken at v_o2, with R_C1 removed. Then we have an emitter follower driving the collector of the second transistor, which forms a common-base (this input is grounded) amplifier. This circuit is good for very high frequencies, for reasons that we shall explore elsewhere. This circuit uses feedback, of course, though we did not use feedback analysis.
Construct and test a differential amplifier using R_C = 4.7k, R_E = 470Ω. Choose R_S so that the collector current in each transistor is about 1 mA, and use a ±12V supply. The single-ended differential gain should be about 5, the common-mode gain about 0.5 and the input impedance at one input about 100k. (How did I get these numbers?). The actual differential gain is a little smaller than 5, because the current source for the emitters is not a good one. The input source can be a buffered potentiometer.

 

A differential amplifier can be constructed using an op-amp, as shown at the right. An op-amp is a differential amplifier itself, but its gain is far too high and frequency dependent to be used as such. The inverting and noninverting inputs are shown by v- and v+. The formula for the differential gain is easily obtained by considering the noninverting input grounded, which means the op-amp tries to keep both its inputs at zero, so the feedback on the inverting side is like a lever with lengths R₁ and R₂ (since the same current flows in both resistors, of course). The common-mode gain is easily seen to be zero, since the inputs go up together if the output voltage is zero. Of course, the actual common-mode gain will not be zero because of various small inequities, both in the resistors and in the op-amp. I tested such a circuit with a 411 op-amp, using R₁ = 10k and R₂ = 100k, for a differential gain of 10 (20 dB). Using 5% resistors, the common-mode gain was 0.029, and with 1% resistors, it was 0.019. The common-mode rejection ratio, CMRR, was, therefore, 10/0.019 = 526 or 54 dB.
If you put a 100Ω resistor between the input terminals of the amplifier I tested, the result is a current sensor with a sensitivity of 1 V per mA that can be used to observe the current at any point with an oscilloscope, which must sense with ground as one terminal. The differential amplifier removes this limitation, which is often quite annoying.
http://mysite.du.edu/~etuttle/electron/elect8.htm
Rooselvet Ramirez EES

The CC-CE, CC-CC, and Darlington Configurations

The CC-CE, CC-CC, and Darlington Configurations

The Darlington pair – CC-CC configuration

Let's consider the circuit of fig. 41, where the biasing components are omitted.

If we suppose that T₁ º T₂ and that they are equally biased, let's compute the voltage gain and input resistance:

 

 Input resistance:

that leads to 

If b » 2, we have

and if g_m R_E >> 1, we may write the approximate value of A_v:

which is the same expression we get for the single transistor emitter follower.

But the input resistance, if b >> 1 and R_E >> 11/g_m is:

much larger than the value b R_E, that is the approximate value we get for a single transistor.

In the same way, the short-circuit current gain is (b +1)² much larger than (b +1) that the single stage has.

Finally, the output resistance is the same in both cases (1/g_m), if the first base is connected to ground.

Probably, the most interesting result is that the two transistor montage can be seen as one only transistor where the three terminals (B, C, E) are respectively, the first base, both collectors and the second emitter and displays a large current gain, typically b ². However, this is not completely true because in general the two transistors are very different being common that the first is a high b small signal transistor while the second is a low b power transistor.

We may conclude that this circuit has approximately the same voltage gain as a simple CE, but a much larger input resistance (

b times larger).

However, as the internal ouput resistance is halved (r_o / 2), the maximum possible gain is smaller than what we can get with one only transistor.

Therefore, this circuit has the required characteristics for the intermediate stage of an OpAmp. However, the high frequency response is deficient. In fact, C_m of T₁ is subject to a very strong Miller effect.

Common Emitter Darlington configuration

In spite of what has just been said, we will admit, for the sake of simplicity, that both transistors have the same characteristics and biasing point. Then, let's consider the schematic of fig. 42.

Input resistance:

 Voltage gain:

and

We may conclude that this circuit has approximately the same voltage gain as a simple CE, but a much larger input resistance (b times larger).

However, as the internal ouput resistance is halved (r_o / 2), the maximum possible gain is smaller than what we can get with one only transistor.

Therefore, this circuit has the required characteristics for the intermediate stage of an OpAmp. However, the high frequency response is deficient. In fact, C_m of T₁ is subject to a very strong Miller effect.

CC-CE configuration

Fig. 43 represents the CC-CE circuit and its small signal equivalent. This is very similar to the circuit we just analysed (the Darlington montage) except for the fact that the two collectors are not connected.

fig. 43 - CC-EC configuration; (a) simplified schematic; (b) small signal equivalent circuit

Again, for the sake of simplicity, we will admit that T₁ and T₂ are equal and equally biased.

Input resistance:

Voltage gain:

and

This circuit presents the same gain and input resistance as the CE Darlington transistor. However the maximum voltage gain is twice as large, since the output resistance (r_o) is doubled.

Though, the most significant change concerns the bandwidth. As the first stage (CE) has a good high frequency response, as we have seen before, and the Miller effect upon C_m of the second transistor does not limit much since it is charged by the low output resistance of the emitter follower the frequency behaviour of the circuit is quite good.

This is why this montage is quite common in the intermediate stage of general purpose OpAmps.

We have been referring to the common configurations of general purpose OpAmps. In general they still have a last stage that should satisfy two requirements: to have a high input resistance not to degrade the voltage gain of previous stages and have a low output resistance to be able to drive the output load. The voltage gain does not need to be high, since the two previous stages are able to provide it. Therefore, these are the characteristics we expect to find in an emitter follower circuit.

 http://paginas.fe.up.pt/~fff/eBook/MDA/MDA.html

 Rooselvet Ramirez  EES