Noise figure (NF)
is a measure of degradation of the signal-to-noise ratio (SNR), caused by components in a radio frequency (RF) signal chain. The noise figure is defined as the ratio of the output noise power of a device to the portion thereof attributable to thermal noise in the input termination at standard noise temperature T0 (usually 290 K). The noise figure is thus the ratio of actual output noise to that which would remain if the device itself did not introduce noise. It is a number by which the performance of a radio receiver can be specified.
The noise figure is the difference in decibels (dB) between the noise output of the actual receiver to the noise output of an “ideal” receiver with the same overall gain and bandwidth when the receivers are connected to sources at the standard noise temperature T0 (usually 290 K). The noise power from a simple load is equal to kTB, where k is Boltzmann's constant, T is the absolute temperature of the load (for example a resistor), and B is the measurement bandwidth.
This makes the noise figure a useful figure of merit for terrestrial systems where the antenna effective temperature is usually near the standard 290 K. In this case, one receiver with a noise figure say 2 dB better than another, will have an output signal to noise ratio that is about 2 dB better than the other. However, in the case of satellite communications systems, where the antenna is pointed out into cold space, the antenna effective temperature is often colder than 290 K. In these cases a 2 dB improvement in receiver noise figure will result in more than a 2 dB improvement in the output signal to noise ratio. For this reason, the related figure of effective noise temperature is therefore often used instead of the noise figure for characterizing satellite-communication receivers and low noise amplifiers.
In heterodyne systems, output noise power includes spurious contributions from image-frequency transformation, but the portion attributable to thermal noise in the input termination at standard noise temperature includes only that which appears in the output via the principal frequency transformation of the system and excludes that which appears via the image frequency transformation.
The noise factor of a device is related to its noise temperature Te:
Rooselvet Ramirez CAF
This makes the noise figure a useful figure of merit for terrestrial systems where the antenna effective temperature is usually near the standard 290 K. In this case, one receiver with a noise figure say 2 dB better than another, will have an output signal to noise ratio that is about 2 dB better than the other. However, in the case of satellite communications systems, where the antenna is pointed out into cold space, the antenna effective temperature is often colder than 290 K. In these cases a 2 dB improvement in receiver noise figure will result in more than a 2 dB improvement in the output signal to noise ratio. For this reason, the related figure of effective noise temperature is therefore often used instead of the noise figure for characterizing satellite-communication receivers and low noise amplifiers.
In heterodyne systems, output noise power includes spurious contributions from image-frequency transformation, but the portion attributable to thermal noise in the input termination at standard noise temperature includes only that which appears in the output via the principal frequency transformation of the system and excludes that which appears via the image frequency transformation.
Definition
The noise factor of a system is defined as:The noise factor of a device is related to its noise temperature Te:
Rooselvet Ramirez CAF
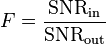






 ,
,

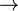
 .
. ,
,



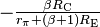

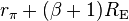


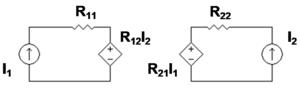
 . As expected, when
. As expected, when  is increased, the input impedance is increased and the voltage gain
is increased, the input impedance is increased and the voltage gain  is reduced.
is reduced.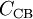 appears like a larger parasitic capacitor
appears like a larger parasitic capacitor  (where
(where  where
where  is the
is the  (e.g., by using emitter degeneration).
(e.g., by using emitter degeneration).